Le plus court chemin & la rivière !

1. Rentrer au château par la rivière !

Mario doit rentrer à son château. Avant cela, il doit passer par la rivière. La question est simple : quel trajet doit-il faire pour parcourir le moins de distance possible ? Autrement dit, par quel point de la rivière doit-il passer ?
Pour mieux comprendre, voici un schéma :

Mario peut donc passer par n’importe quel point de la rivière. Convenons d’une chose qui j’espère est évidente : il va se déplacer en ligne droite jusqu’à la rivière, et en ligne droite de la rivière jusqu’au château. Par exemple, suivre le trajet suivant :

J’ai affiché les distances des 2 petits trajets, puis la distance totale parcourue. Si je change le point A sur la rivière, j’obtiens un résultat différent :

On voit que ce second trajet est moins intéressant car plus long.
Mais alors, je repose la question : comment faire pour minimiser la distance ?

Cela semble difficile… je vous laisse y réfléchir un peu, avant de vous présenter la solution (juste en dessous, n’en lisez pas plus si vous souhaiter y réfléchir !).

____________________________________________________________________________

Pour répondre à ce problème, il faut en fait utiliser un résultat très simpliste, que nous avons déjà évoqué : « La distance la plus courte entre 2 points est…la ligne droite ! ».

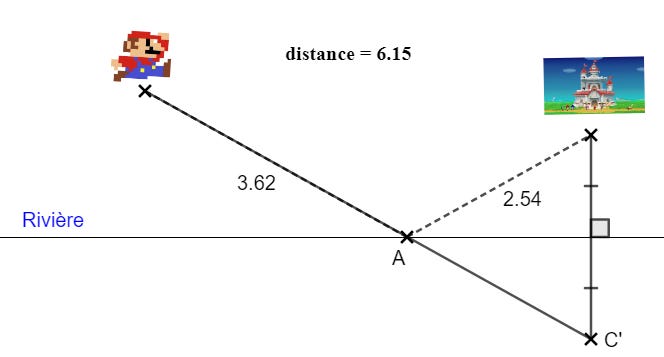
Nous allons commencer par tracer le symétrique du château par rapport à la rivière, j’appelle C’ ce point (le symétrique est sur la perpendiculaire à la rivière, et est à égale distance de la rivière.) Je trace ensuite le trajet de Mario jusqu’au symétrique C’.

Pour minimiser la distance, il faut alors passer par le point A de la rivière, qui est celui par lequel passe le chemin précédemment tracé !

En effet, le trajet de Mario au point C’ est le plus court (la ligne droite !). Or, la distance de A à C’ est la même que celle de A au château (cela vient du fait que nous avons tracé le symétrique). Finalement, c’est bien le trajet le plus court ! Ici, cette distance minimale vaut 6,15 !

De façon générale, pour avoir le plus court chemin pour aller d’un point A à un point B en passant par une droite (d), il faut :

• Tracer le symétrique B’ de B par rapport à (d).

• Tracer le segment [AB’].

• Nommer C le point d’intersection entre le segment précédent et (d).

• Le plus court chemin consiste alors à faire le trajet de A à C puis de C à B.

2. Attention à la ligne droite !

Je tiens à rectifier une affirmation que nous avons faite : « Le trajet le plus court entre 2 points est la ligne droite ». Oui…mais !

En fait, ce résultat est vrai en géométrie « classique », ce dont nous avons l’habitude de faire à l’école, sur des plans.

Sur des globes par exemple, ceci n’est plus vraiment valable. Il y a une situation qui permet de bien l’illustrer : les trajets des avions. Voici différents parallèles sur le globe (représentés à plat sur un planisphère). Il y a en particulier le 43e, passant par Toulouse et Toronto.

Voici maintenant le trajet suivi par les avions pour rejoindre ces 2 villes, qui bien évidemment est minimal (pour économiser le carburant) :

Oui, on ne semble plus suivre les lignes droites du planisphère…