Note : cet article faisant office de “mini-cours”, celui-ci est un peu long et pourrait ne pas s’afficher entièrement sur un mail. Pour une meilleure lecture, retrouvez-le sur le blog :
Autour des triangles - l'article de blog
Le triangle est l’une des figures Mathématique les plus simples qui soit. Leur étude en est assez sommaire. Classiquement, on apprend la formule pour calculer leur périmètre et leur aire. Mais il y a tout de même quelques faits peu connus (du moins peu enseignés) qui méritent d’être mis sur le devant de la scène !
1. L’aire du triangle : prendre de la hauteur
Reprenons du début. Un triangle est une figure plane (en 2D) formée par 3 points distincts (ses sommets) non alignés et les segments qui les relient (les côtés).
Deux côtés d’un triangle forment un angle et puisqu’il y a 3 paires de côtés on dénombre… 3 angles : le tri angle.
Le triangle est le polygone le plus simple qui soit, et en un sens le plus fondamental car il permet via des découpages de calculer les aires de tous les polygones (j’y reviendrai dans un prochain article).
Remarquons que pour qu’un triangle puisse exister, les longueurs de ses côtés ne peuvent pas être quelconques. Par exemple il n’est pas possible de construire un triangle de côté 8, 3 et 4.
Vous pouvez vous en convaincre en regardant ce schéma. Les côtés AC et CB étant à eux 2 plus courts que le côté AB, il ne sera pas possible de placer le C de part et d’autre de A et B (les 2 segments ne peuvent se rejoindre).
Il aurait fallu que ces 2 côtés (les 2 plus petits) soient à eux 2 plus grands que le 3e (le plus grand). Ceci se traduit par l’inégalité : AB ⩽ AC + CB.
On note cette relation inégalité triangulaire, qui est la condition à respecter pour qu’un triangle puisse exister.
Lançons-nous dans les calculs d’aires comme étudiés au collège. Tout d’abord avec le cas du triangle rectangle.
Il est aisé de voir que ce dernier correspond à la moitié d’un rectangle de longueur AB et largeur AC.
Puisque l’aire du rectangle est AB × AC celle du triangle sera sa moitié :
Dans un triangle, on appelle hauteur le segment reliant un sommet au côté opposé de façon perpendiculaire. Par exemple ici en prenant BC pour la base on obtient la hauteur AB.
Ainsi nous pouvons écrire que :
Ce raisonnement se généralise en fait à n’importe quel triangle, en construisant une hauteur et en effectuant le bon découpage pour obtenir un rectangle.
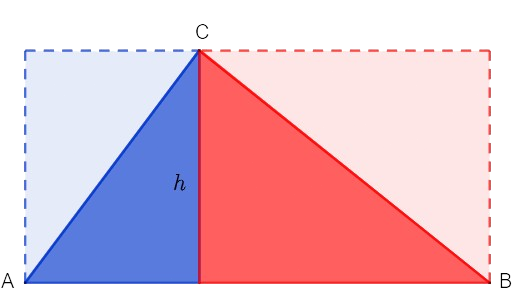
Pour obtenir l’aire du triangle ABC, on peut prendre comme base AB et construire la hauteur correspondante. On voit alors qu’en doublant les 2 moitiés de triangle obtenues, on obtient un rectangle dont on peut calculer l’aire : AB × h.
Pour avoir l’aire, on en prend la moitié : (AB × h) : 2.
La formule se généralise pour chaque triangle :
2. Des bases parallèles !
Regardons une conséquence amusante de ce résultat. Les droites (AB) et (CD) sont parallèles et l’on cherche à savoir lequel des 2 triangles a la plus grande aire. Nous n’avons cependant aucune mesure.
Oui, mais ! Considérons la base AB commune aux 2 triangles. Je vous laisse vous convaincre que les hauteurs associées pour chacun des 2 triangles seront de même longueur (il s’agit de celle d’un segment joignant (AB) et (CD) de façon perpendiculaire).
Puisque pour les 2 triangles on a une base de même longueur et les hauteurs de même longueurs, les aires sont donc forcément identiques !
On peut en fait déplacer les points C et D n’importe où sur la droite du haut, les triangles conserveront toujours la même aire !
3. Avec 2 côtés et un angle
La formule connue pour calculer l’aire d’un triangle souffre d’un défaut : il n’est pas toujours facile de connaitre la mesure d’une hauteur. En pratique, il est plus aisé de connaitre les mesures des côtés et/ou celles des angles. Nous allons voir que nous pouvons en fait facilement contourner ce problème.
Partons de la figure suivante. Les objets en rouges sont ceux dont nous connaissons les mesures (2 côtés et l’angle qu’ils forment). On a tracé la hauteur [CH] de longueur h.
Grâce à la trigonométrie dans le triangle rectangle ACH rectangle en H (souvenirs du collège), nous pouvons exprimer la longueur h en fonction de AC et . On trouve que :
De la formule Aire = ½ × (base × hauteur) on peut en déduire une nouvelle en remplaçant la hauteur par la valeur trouvée :
Remarquez qu’il s’agit des 3 données connues !
Nous avons donc une nouvelle formule, utilisable en connaissant 2 longueurs et l’angle associé !
4. L’aire du triangle en fonction de ses 3 côtés
Pour la formule précédente, nous avons utilisé une mesure d’angle pour connaitre l’aire. Serait-il possible de la calculer en utilisant seulement les longueurs des 3 côtés ? J’imagine que vous n’avez jamais vu une telle formule.
Pourtant, si je vous donne 3 longueurs, vous pouvez vous convaincre qu’il est possible de ne construire qu’un unique triangle ayant ces 3 mesures pour côté (à condition que ces longueurs respectent l’inégalité triangulaire). Pour être plus précis, 2 triangles ayant les 3 mêmes longueurs sont identiques en ce sens que l’on peut transformer le 1er en le 2nd avec des transformations géométriques simples (rotations…).
Si 3 longueurs permettent de construire un unique triangle, il est donc clair que l’aire de celui-ci est déterminée par ces longueurs.
Prenons le cas du triangle équilatéral ABC et notons a la longueur de ses côtés et traçons une hauteur.
Par découpage, son aire est celle du rectangle de longueur CH et de largeur AH.
Calculons AH à l’aide de Pythagore :
AC² = CH ² + AH ² Or AC = a et AH = a/2
et l’on déduit que :
L’aire du triangle est donc finalement :
Et voilà, nous avons une formule pour l’aire du triangle équilatéral uniquement à partir de la longueur de ses côtés !
Pour le cas général, c’est en fait aussi possible mais la formule est plus complexe ! Je vous la donne tout de même.
On considère un triangle dont les 3 côtés mesurent a, b et c. On note d son demi-périmètre : d = (a+b+c) / 2.
On a alors l’aire du triangle donnée par la formule de Héron :
5. Le théorème de Pick
Il existe un dernier cadre assez amusant dans lequel nous pouvons facilement calculer des aires de triangle, et cette fois-ci sans connaitre la moindre longueur ou le moindre angle !
Il s’agit de considérer des triangles dont les sommets sont situés sur les points d’une grille comme ci-dessous.
L’unité de mesure est ici la longueur d’un côté d’un carreau.
Notons i le nombre de points intérieurs (en rouge) du triangle et b le nombre de points sur le bord du triangle (en bleu). Le théorème de Pick affirme que :
tout simplement !
Par exemple pour le triangle ABC, on a i = 8 et b = 3 donc son aire vaut 8 + 3/2 – 1 = 8,5.
Pour le triangle DEF on a i = 3 et b = 5 donc son aire est de 3 + 5/2 – 1 = 4,5.
Le théorème de Pick fonctionne en fait pour n’importe quel polygone construit sur une grille !
Si vous êtes motivés, vous trouverez facilement plein de démonstrations sur internet. Elles sont plus pénibles à écrire qu’à comprendre, alors vous pouvez tenter d’y jeter un coup d’œil
6. Un petit bilan !
Bien qu’il s’agisse d’une forme simple, le triangle recèle quelques belles propriétés méconnues !
Il existe plusieurs façons d’en calculer l’aire, en fonction des données connues :
Pour un triangle “quelconque”, la formule classique :
\(aire=\dfrac{base×hauteur}{2}\)Avec un angle, 2 longueurs AB et AC ainsi que l’angle α entre les 2 côtés :
\(aire = \dfrac{AB × AC sin(α)}{2}\)Avec les 3 longueurs des côtés, notées a, b et c et d le demi-périmètre :
\(aire=\sqrt{(d(d-a)(d-b)(d-c))}\)Pour un triangle construit sur une grille, en notant i le nombre de points intérieurs et b celui de points sur le bord :
\(aire = i + \dfrac{b}{2} – 1 \)